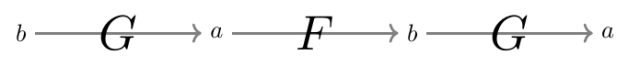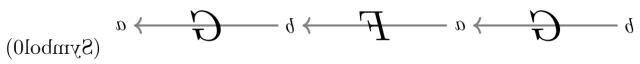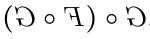There is a body of results in higher category theory which this expository blog post will present you a toy version of.
Not to bias this post too much, and not to slight said body of results (they actually are much more substantial than the following story might make you believe), I will not say what technical term said results usually go by. Here I will call them robustness theorems. Disclaimer: this is non-standard terminology.
What I really mean is a term similar to the term Tauberian theorems in number theory: an umbrella term binding together a bundle of similar results.
So again, I won’t tell you what these theorems are usually called—only so much: (0) the analogy with Tauberian theorems is rather apposite (the two bundles of results are spiritually quite similar) in that this is about giving a reasonable meaning to expressions (1) I here will call them by the unusual term robustness theorems.
So what is the simplest robustness theorem, the toy robustness theorem?
To my mind, arguably, it is the following.
Suppose you know a person P.
Suppose it is understood what the two symbols  and
and  mean in the communication between you and P. That is, you know how to interpret both
mean in the communication between you and P. That is, you know how to interpret both  and
and  .
.
However, the symbols  and
and 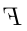 are considered nonsense; you will never be satisfied to have made sense of something P sends to you unless you have assembled a well-formed expression involving only
are considered nonsense; you will never be satisfied to have made sense of something P sends to you unless you have assembled a well-formed expression involving only  and
and  .
.
Now suppose a person P sends to to you a string of symbols.
Suppose what you are being flashed on your display is
(Symbol0)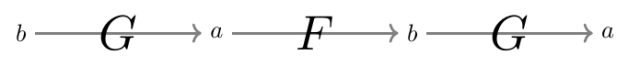
Now what to make of that? This symbols itself is evidently sort-of-a-finite-string
of symbols, quite-string-like indeed. But what is it supposed to mean?
In principle, of course, you are free to interpret in any way you want.
You might interpret it as true, for example.
Yet this is not the intended interpretation.
There is something that this symbol was made for.
It might not surprise you that (Symbol0) is intended to represent one morphism  in a category
in a category 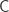 , with
, with  intended to be assembled from the morphisms
intended to be assembled from the morphisms  and
and  .
.
It will also not surprise you that here, ’assembled from’ does not mean
’assembled in any way you like’, not even ‘in any meaningful way’ .
While logically there is no reason why the above geometric picture must mean the morphism 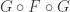 , there are customs regarding how the assembling should work, and those demand the interpretation
, there are customs regarding how the assembling should work, and those demand the interpretation 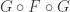 .
.
In principle, you could define any crazy interpretation of the above symbol, for example  would also define a morphism
would also define a morphism 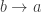 there is nothing logically wrong with such a deviant rule, but it does not give the intended interpretation. (It would be similar to having a private rule to interpret the string ‘seventeen’ to mean the number
there is nothing logically wrong with such a deviant rule, but it does not give the intended interpretation. (It would be similar to having a private rule to interpret the string ‘seventeen’ to mean the number 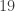 .)
.)
In short, we have to give a rule (for brevity, we will take ‘rule’ to be a convenient monosyllabic synonym for the tetrasyllabic ‘algorithm’) for how to assemble expressions like (Symbol0) into one morphism of a category (to be precise: this, too, is an arbitrary choice-of-semantics that we make here: for the sake of this expository post, we just decide to only interpret expressions in humble 1-categories, while the robustness theorems apply to higher categories), and this rule should be generally applicable and, logically-consistent.
Let us try to make such an interpretation-rule:
(R0) Start at the left of the expression-to-be-interpreted, move rightwards, select the first letter you hit, hold it, interpret it as the name of a morphism in a 1-category 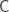 , go on moving rightwards until the next,
, go on moving rightwards until the next,
hold it, interpret it accordingly, compose the two you morphisms you hold via the composition-function  of
of 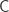 to get a single morphism, hold it, go on moving to the right, repeat all of this, until you have reached the right-hand end of the symbol. The morphism-that-is-the-iterated-composite is the interpreation of the expression.
to get a single morphism, hold it, go on moving to the right, repeat all of this, until you have reached the right-hand end of the symbol. The morphism-that-is-the-iterated-composite is the interpreation of the expression.
Applied to (Symbol0), (R0) gives us the interpretation 
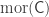 .
.
Now comes the catch, an alternative scenario: suppose you were being flashed—perhaps due to some technical malfunction, or because you are standing on the other side of a window pane that P is scribbling (Symbol0) on—the symbol
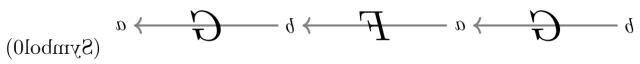
Now what sense to make of that?
Being human, you might recognize this to be just the mirror-image of (Symbol0), and derive your interpretation from this observation, and the above procedure.
Yet, for the sake of argument, suppose you are being not very perceptive today, and perhaps currently so much in awe of the idea of non-text syntax that you cannot do better than to timidly and rigidly stick to your interpretationi rule (R0) when interpreting 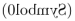 .
.
You are then led to interpret 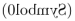 to the composite
to the composite
(TemporaryInterpretation0) 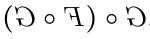
which, however, does not yet make sense under the hypotheses stipulated in the beginning (namely that the symbols 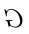 and
and 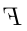 in an interpretation of P’s messages are not acceptable to you).
in an interpretation of P’s messages are not acceptable to you).
Then there are the two following reasonable interpretation-options open to you, to give acceptable meaning to (TemporaryInterpretation0): either you reflect each variable in 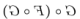 separately to arrive at
separately to arrive at  , which happens to be the same as what you interpreted (Symbol0) to.
, which happens to be the same as what you interpreted (Symbol0) to.
However, it is also reasonable, and arguably more reasonable, that you simply reflect the expression 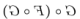 from (TemporaryInterpretation0) in its entirety about the vertical axis to arrive at
from (TemporaryInterpretation0) in its entirety about the vertical axis to arrive at 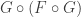 .
.
So, in summary, in two scenarios you ended up with the interpretation  , while in another scenario (in a sense, in one-out-of-three possible scenarios for the communication process), you ended up with
, while in another scenario (in a sense, in one-out-of-three possible scenarios for the communication process), you ended up with 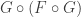 .
.
Fortunately, the usual axioms of 1-category theory contain an equality statement
expressing associativity of composition, telling you that, in particular,  .
.
So if you interpret (Symbol0) in any one of the above ways,
- the axioms of 1-categories are robust to some of the vagaries of communication, provided that customary interpretation rules are used,
in that
- the resulting morphisms came out the same, despite your rigid rule (R0),
and despite the transmission error that handed you a mirror image, and despite the arbitrary choice of what to make of reflected letters.
We hasten to add that, needless to say
- no non-trivial axiomatic system can be robust against all possible non-customary and possibly crazy interpretation rules (like, say, a rule which would interpret the mirror-image
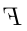 to mean
to mean  ).
).
One can illustrate this above story in an informal ‘diagram’ (disclaimer: this
diagram is not known to be a mathematical object; the arrows have different sorts; not all arrows in the following are claimed to be morphisms of a category):
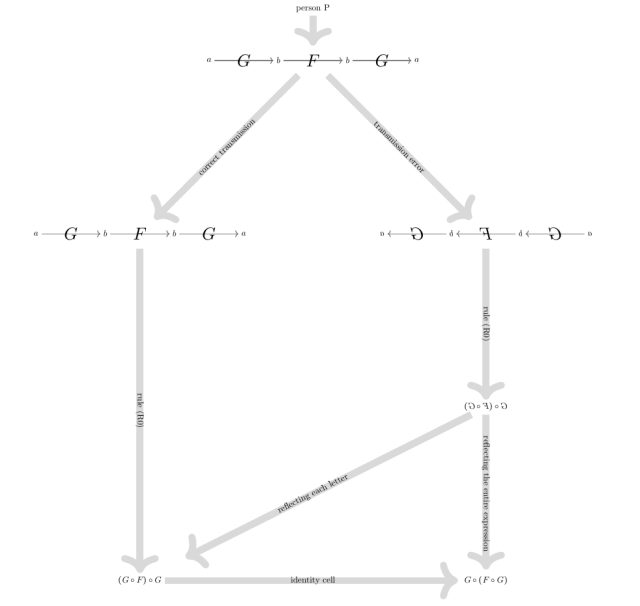
Here, ‘identity cell’ is a technical term, more or less synonymous with ‘equality’. (In case you are interested, ‘equality’ rather means something like a logical judgement, with which one just declares two things to be equal, while ‘identity cell’ means something like evidence, emphasizing that there is some specified amount of data in a standardized form, witnessing that the two things in question are equal).
To sum up, we have our toy robustness theorem:
- the axioms of 1-category theory make the transmission of the one-member class of symbols
 (Symbol0)
(Symbol0)  robust against (0) rather arbitrary distortions of the symbol by Euclidean plane isometries, and quite some more distortions, and (1) a rigid interpretation rule like (R0). The resulting morphism of the category is exactly the same.
robust against (0) rather arbitrary distortions of the symbol by Euclidean plane isometries, and quite some more distortions, and (1) a rigid interpretation rule like (R0). The resulting morphism of the category is exactly the same.




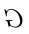 and
and 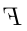 are considered nonsense; you will never be satisfied to have made sense of something P sends to you unless you have assembled a well-formed expression involving only
are considered nonsense; you will never be satisfied to have made sense of something P sends to you unless you have assembled a well-formed expression involving only